The Influence of Seasonal and Latitudinal Insolation Distribution on Climate Variability over the Past 1.5 Ma

This is a group project I led during summer 2023 at an international research summer camp hosted by Shanghai Jiaotong University, which was published on 11th Academic Conference of Geology Resource Management and Sustainable Development 2023 (DOI:10.52202/073371-0113).

Abstract: The Quaternary Glacial-Interglacial Cycle (G-IG cycle) is primarily driven by variations of the Earth’s Orbit. Astronomical parameters, including precession, eccentricity, and obliquity, affect global climate by modulating the seasonal and latitudinal distribution of insolation. However, a quantitative assessment of this correlation remains lacking. This essay aims to investigate the following using paleoclimate records over the last 1.5 Ma: 1) The relationship between insolation seasonality and the G-IG cycle; 2) The relationship between Latitudinal Insolation Gradient (LIG) and the G-IG cycle; 3) The combined effects of seasonal and latitudinal insolation variations. The clear matching between the rate of G-IG transformation, seasonal and latitudinal insolation variation provides a crucial supplement to the traditional Milankovitch theory, and also suggest a new perspective for investigating the connection between astronomical calculation and records in paleoclimate data. Additionally, we discuss the indirect and indirect control of insolation on the shorter-term Millennial Climate Variability (MCV) using high-resolution marine sediment data. Illuminating these orbital forcing mechanisms contributes to a deeper understanding of climate dynamics and also provides a reference for their potential implications on future climate change.

Keywords: Orbital forcing, Insolation gradient, Interglacial, Seasonality, Millennial Climate Variability

1. Introduction

The alternation between glacial and interglacial periods over the Quaternary period (last 2.6 million year) is shown clearly in paleoclimate records such as ice cores [1] and marine sediments [2]. The most accepted explanation for this alternation is the Milankovitch theory, which highlights the significance of three orbital parameters: obliquity, precession and eccentricity [3]. These forcings impact the climate not by altering the total amount of energy reaching the top of the atmosphere annually, but by causing variations in the latitudinal and seasonal distribution of insolation [4,5]. The variation in seasonal insolation is mainly driven by the combined effects of eccentricity and precession, primarily at a cycle of 23,000 years [3]; meanwhile, changes in tilt could enhance or suppress the magnitude of change, particularly at high latitudes [6]. On the other hand, the LIG is driven by obliquity in summer and precession in winter [7].

Plenty of studies have investigated the linear and non-linear correlation between the orbital parameters and G-IG cycles [8–11], as well as the possible mechanism by which insolation seasonality or latitudinal insolation gradient (LIG) lead to global or local climate changes [7,12–14]. However, there is a lack of quantitative evaluation regarding the numerical correlation between insolation distribution and G-IG the cycles. The mechanism by which these temporal and spatial insolation variations drive global climate changes is poorly understood as well. This paper aims to examine such correlation over the past 1.5 Ma by comparing the rate of change of relative sea levels with the insolation data.

In addition to orbital-scale climate change, millennial events are of great significance as well, as they include a series of abrupt climate changes within the Dansgaard-Oeschger Cycle. The cycle has a sawtooth pattern, typically with an abrupt warming occurring within a few decades and a gradual cooling before a rapid return to a cold state [15]. These millennial variabilities are often thought to be closely linked to internal forces such as ice sheet dynamics [16–18], sea ice feedbacks [19–22] and the Atlantic Meridional Overturning Circulation (AMOC) [23–26]. Nevertheless, in terms of the long-term trend, MCV’s dependence on the background climate state is also notable and can be seen as an indirect outcome of the variation of incoming insolation [27–29]. During some particular period, the insolation can even directly control MCV, which is supported by recent modelling [30]. This article would examine the relationship using high-resolution paleoclimate data and statistical methods.

2. Method

2.1 Insolation Data

The equation to calculate the daily amount of incident solar radiation at latitude ∅ is:

Where τ represents the time in days, S_0 is the solar constant, ρ is the mean value of Sun-Earth distance, ω_0 is the hour angle of the Sun at sunset, and δ is the apparent solar declination. [31] Referring to the work of Laskar et al. [32], we use Acycle software [33] to calculate the difference in insolation at 65°N on the summer solstice (21 June) and winter solstice (21 December) as an indicator of seasonal insolation variation (ΔSEASON). Additionally, the difference between the annual mean insolation reaching the equator and the north pole is calculated to assess the latitudinal insolation gradient (ΔLAT).

2.2. Indicator for the Glacial-Interglacial Cycle

Relative sea level (RSL) data reconstructed by Berends et al. (2021) was used as an index of the glacial-interglacial climate variability [34]. To remove noise, A Butterworth filter [35] with a cut-off of 0.2 kyr was applied. By taking the first derivative for the filtered data (using Acycle), we get an insight into the rate of each regression and transgression, and hence the rate of each deglaciation and cooling period (see Figure 1).

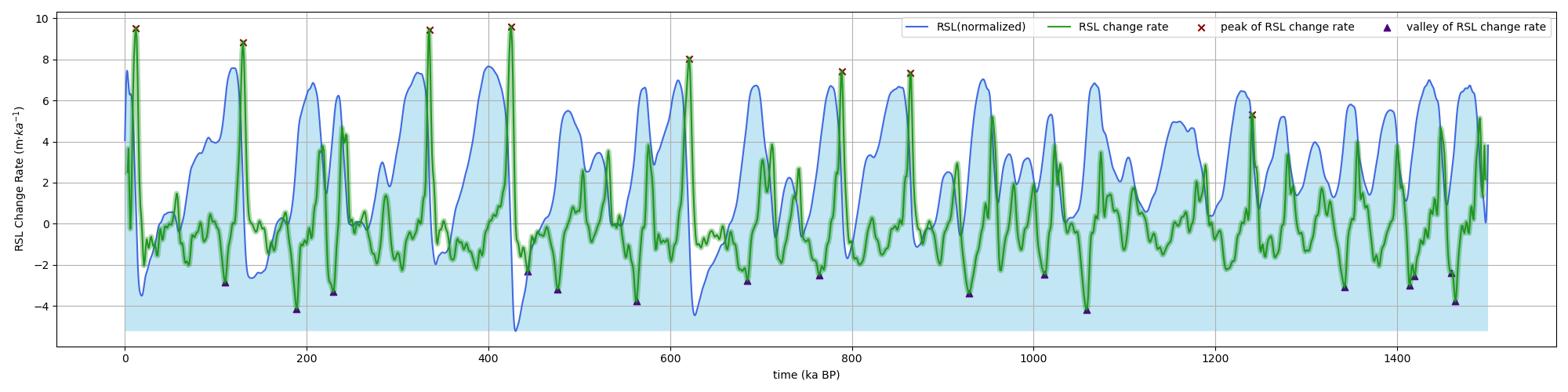
2.3. Indicator for the Millennial Climate Variability

To study the MCV, we employ the δ18O record of G. bulloides at Site U1385 [36]. We first apply a high-pass filter [35] to remove orbital frequencies and extract suborbital variability. Values that are less (or greater) than 1 SD (standard deviation) from the mean are considered to be stadial (or interstadial) events. The total number of millennial events (stadial and interstadial) per 10,000 years is then counted and plotted as the red curve in Figure 2.

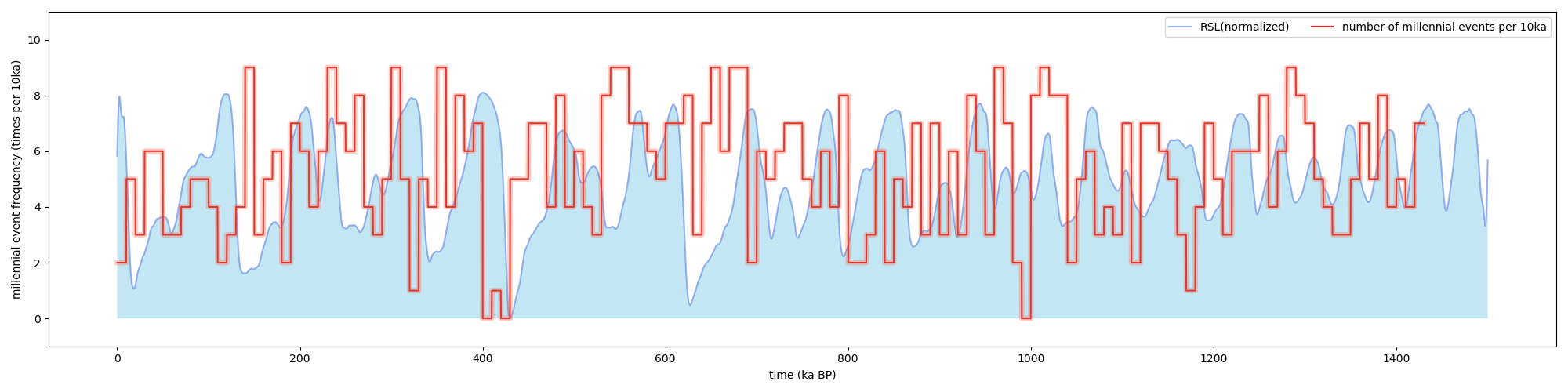
3. Results

The relationships between RSL change rate, seasonal, and latitudinal insolation variation are shown in Figure 3 and Figure 4. Overall, the deglaciation period is more likely to occur when the seasonal difference is large and the latitude gradient is small.

3.1. Insolation Seasonality and the Glacial-Interglacial Cycles

Figure 5 and Figure 6 examine the relationship between sea level variability and the two insolation differences respectively, with the colour of each point reflecting their timing. Figure 5 displays a positive linear correlation between the RSL change rate and the seasonal insolation difference (y=0.04x-19.57,R^2=0.2539,Pearson R=0.504). Great seasonality generally corresponds to the ice loss period, and vice versa. The physical mechanism behind this correlation is that when insolation seasonality is evident, more radiation would reach higher latitudes during summer times, promoting the melting of the ice sheets. The melting will be then accelerated by greenhouse and ice albedo feedbacks [37] and push the Earth into warmer periods. Records from different periods are approximately equally distributed around the regression line, which can demonstrate that the relationship does not change over time. However, there are some outliers, mainly younger than 30 kyr, with much greater sea level variability than others. This may be explained by the extension of the G-IG cycle from 40,000 to 100,000 years since MPT, as this gives the ice sheet more time to accumulate, intensifying and speeding up each deglaciation [38].

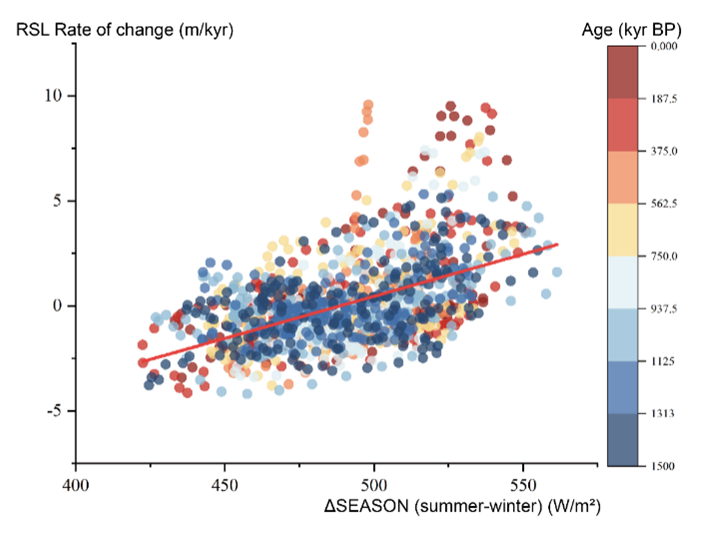
3.2. Latitudinal Insolation Gradient and the Glacial-Interglacial Cycles

Reversely, Figure 6 reveals a negative linear regression: the greater the latitudinal insolation gradient, the more likely the earth would undergo cooling rather than deglaciation (y=-0.29x+56.07〖,R〗^2=0.29901,Pearson R=-0.547). Although there are the scattered young anomalies, probably attributing to the transition from 41 kyr world to 100 kyr world, most points are evenly distributed around the regression line. This provides a compelling support for the “gradient hypothesis” proposed by Raymo and Nisancioglu [39]. The decline of obliquity and rise in LIG is generally followed by increase in equator-to-pole temperature gradient (EPTG) and speed up the poleward transport of moisture [40], both through dynamically impacting storm activities and thermally influencing the fraction of precipitation falling as snow [41]. This mechanism is supported by the excess in deuterium in the Vostok ice core [42] and the GRIP core [43]. Overall, the decrease in high latitude temperature and enhanced delivery of moisture would promote ice sheet growth and hence lead to cooling periods.

3.3. The Collective Impact of Seasonal and Latitudinal Insolation Difference on the Orbital-Scale Climate Variability

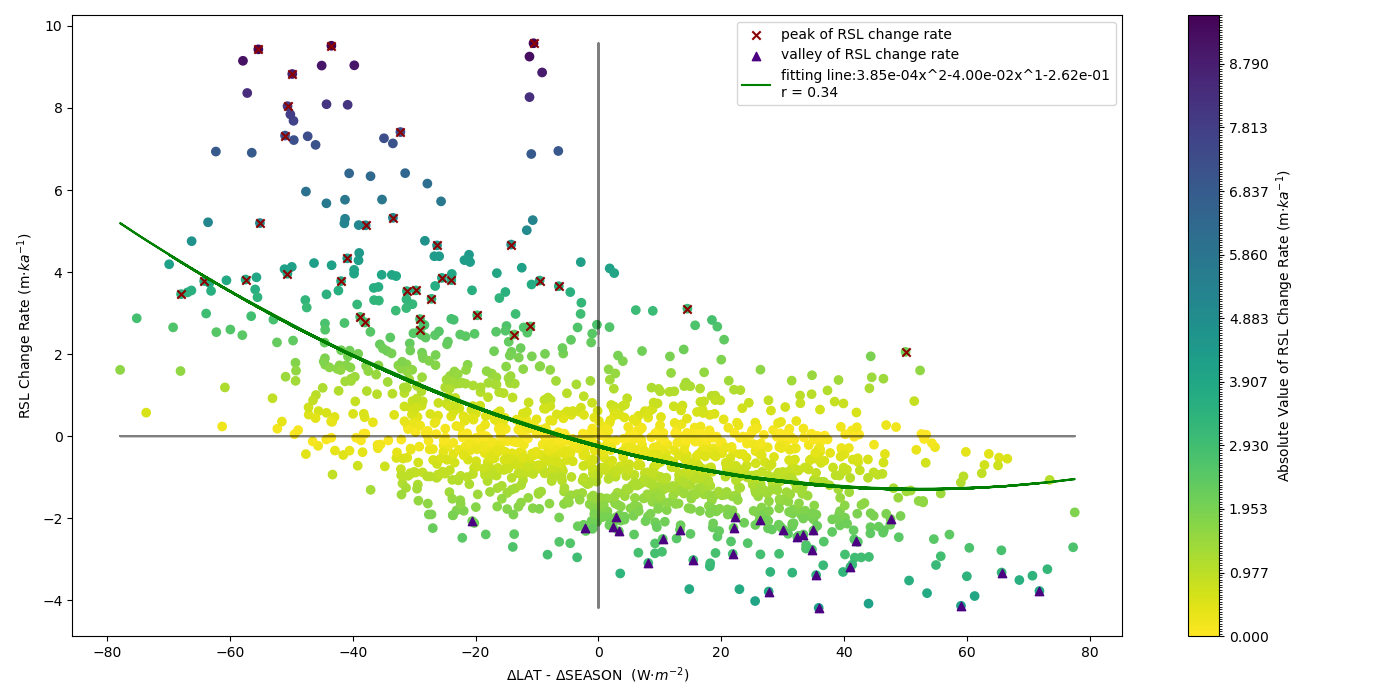
As evident from Figure 3, the peaks of RSL change rate are often aligned with the peak or valley values of seasonal and latitudinal insolation differences. By calculating the difference between the latter two variables (∆LAT-∆SEASON), we explore their collective impacts on the global climate (see Figure 7 and Figure 8).

Figure 7 presents a distinct negative correlation between (∆LAT-∆SEASON) and the RSL change rate. Instances where (∆LAT-∆SEASON) is below the mean value are associated with positive RSL change rate, signifying interglacial periods. The few periods deviating from this negative correlation are highlighted in orange, with generally small amplitudes. Further, Figure 8 displays the curve fitting of this relationship. The majority of data points situate in the second and fourth quadrants, confirming the negative correlation between the variables. Notably, all peak and valley values of RSL change rate, representing deglaciation and cooling periods, are positioned at two extremities of the graph. On the other hand, points in the first and third quadrants exhibit in-phase changes (the orange parts in Figure 7), but their amplitude are minimal, comprising only two peaks and two valleys of the RSL change rate. Overall, Figure 7 and Figure 8 illustrate that the Earth is more likely to enter glacial periods when the latitude insolation gradient is more apparent (hotter tropics, colder poles) and the seasonal insolation difference is more subtle (milder winters and summers).

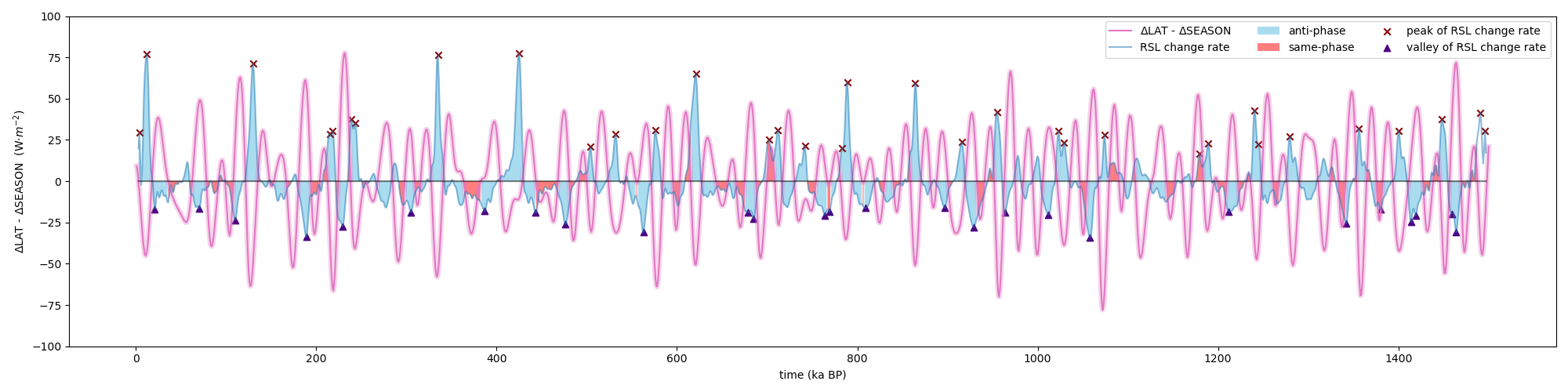
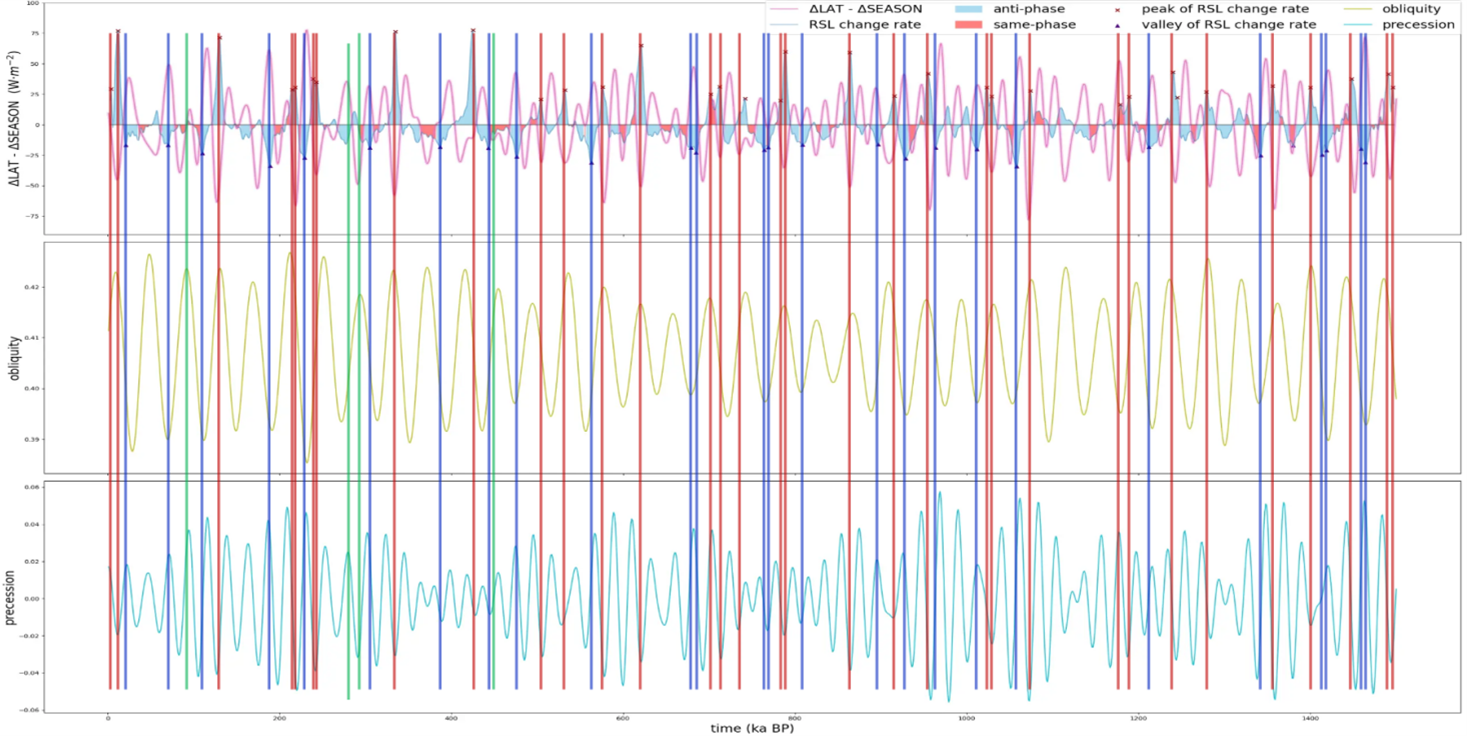
The mechanisms become clearer when we consider the variations of orbital forcings and how they modulate the temporospatial distribution of insolation. Precession is a key forcing controlling insolation seasonality. For instance, when northern Hemisphere summer approaches perihelion, insolation intensifies in summer but diminishes in winter, thus magnifying insolation seasonality. Meanwhile, precession also affects latitudinal insolation variations. When the northern Hemisphere summer is close to perihelion, high latitudes experience accelerated warming, whilst the temperature of low latitude areas decreases because of reasons such as negative cloud albedo feedback in a strengthened monsoon system [44], and the depressed winter sea surface temperature (SST) in low latitude areas which is unable to recover in summer because of the thermal inertia of ocean [45], [46]. Consequently, heightened northern Hemisphere summer insolation could weaken the latitudinal temperature gradient (LTG). By merging these two precession effects with that of obliquity (which inversely relates to ΔLAT), the climate history of the past 1.5 Ma can be categorized into four distinctive scenarios:

1) Firstly, when the Northern Hemisphere summer is close to perihelion and the Earth’s axial tilt is relatively large, ΔLAT decreases, while ΔSEASON increases. As a result, the difference between these two variables (ΔLAT-ΔSEASON) increases, thereby increasing the possibility of entering an interglacial period (shown as the points located in the fourth quadrant of Figure 8, the red vertical lines in Figure 9(a), and the coloured part in Figure 10(a)(e)). The physical explanation for this trend is that warmer tropical winters facilitate the delivery of moisture towards higher latitudes, aiding in the buildup of ice sheets. Meanwhile, the mild summers in high latitudes help preserve the ice from melting. 2) The second scenario is when the Northern Hemisphere summer is near perihelion but the obliquity is small. During this period, ΔLAT decreases due to precession, yet the strengthening effect brought by reduced obliquity overcomes it, resulting in a slight cooling. This leads to both variables being negative, marked by the green vertical line in Figure 9(b), the third quadrant in Figure 8, and the coloured part in Figure 10(c)(g). 3) Likewise, a modest warming occurs when the Northern Hemisphere summer is near aphelion and with a larger axial tilt, reflected by both variables being positive (shown as the purple vertical line in Figure 9(b), the first quadrant in Figure 8, and the coloured parts in Figure 10(d)(h)). Notably, the RSL change rates in the second and third scenarios are generally small, as indicated by the light colors in Figure 8. 4) Lastly, when the Northern Hemisphere summer is near aphelion with a smaller obliquity, ΔSEASON decreases, while the ΔLAT is amplified by the combined effects of precession and obliquity. This leads to an increased (ΔLAT-ΔSEASON) and makes it easier to enter a glacial period, aligning with the “glaciation-friendly” period proposed by Jackson and Broccoli (2003). The scenario is plotted as the blue line in Figure 9, the second quadrant in Figure 8 and the coloured parts of Figure 10(b)(f).

Examining disparities in the spatial and temporal distribution of insolation yields a more coherent understanding of the link between G-IG cycles and the combined effect of orbital signals. This novel approach not only reconciles theoretical calculations with real paleoclimate evidence, but also adds crucial depth to the conventional orbital theory which typically evaluates only individual astronomical forcings.

3.4. Insolation Distribution Control on Millennial Events

Although millennial events are often thought to be the result of internal forces including ice sheets and ocean circulation, external factors such as the total amount of insolation and its temporospatial distribution also play an important role in modulating the timing and frequency of these millennial events [47].

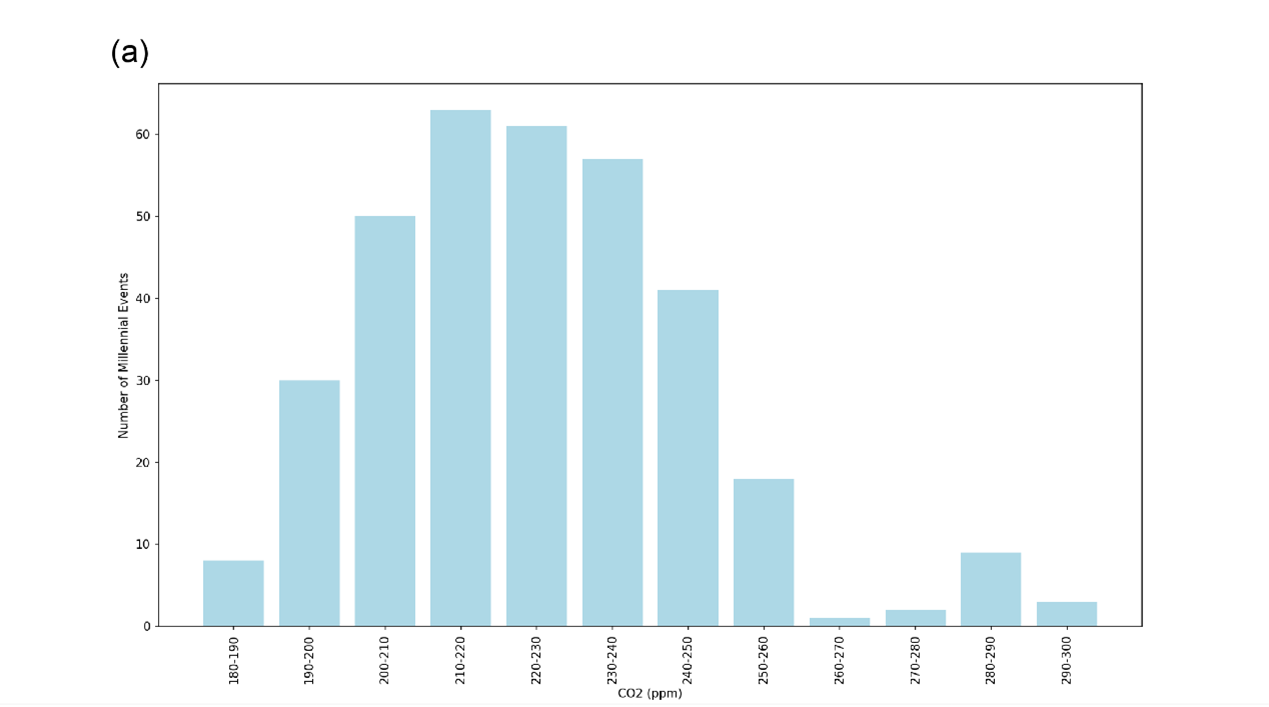
Insolation can indirectly control the timing and frequency of millennial events by regulating the total ice volume. Statistical analysis of all millennial events in the past 1.5 Ma illustrates that there are more of them occurring during the intermediate glacial periods, which proves that the theoretical explanation of the model simulation by [18] can be applied to the MCV pattern during the past 1.5 Ma. This is because both too high and too low insolation would suppress the free oscillations of the thermohaline circulation (THC) [48], whilst during the intermediate glacial periods, only a slight change in ice sheet height is able to trigger abrupt changes in AMOC by altering heat distribution and sea ice concentration in the North Atlantic.

Different from the G-IG cycles, the insolation distribution controls MCV mainly by influencing key millennial triggers such as sea ice, salinity, and AMOC [49-51]. By analysing the cumulative number of millennial events occurring under different insolation distribution scenarios in the past 1.5 Ma, we observe a positive correlation between the millennial event frequency and both ΔSEASON (Figure 11(a)) and ΔLAT (Figure 11(b)). The linear relationship is particularly pronounced during intermediate glacial periods, confirming the findings of Zhang et. Al (2021) [30]. When the insolation seasonality is evident, warmer boreal summers prompt reduced sea ice and increased open-water areas in the subpolar North Atlantic. This could enhance oceanic heat loss during colder winters, which in turn strengthens North Atlantic Deep Water (NADW) formation. However, what is more dominant is the reduced sea-surface salinity as the mean annual net precipitation over the tropical North Atlantic increases. Eventually, the AMOC is weakened, which is a key driver of the abrupt millennial change. On the other hand, with small obliquity and hence considerable latitudinal insolation gradient, low latitudes warm and high latitude cool. Although the enhanced atmospheric moisture export could contribute to NADW formation to some extent, the expanded sea-ice coverage and limited deep convection in high latitudes would eventually lead to weakened AMOC [50].

4. Conclusion

This study aims to investigate the complex relationship between temporospatial differences in insolation distribution and climate variability. In terms of orbital-scale climate changes, the onset of deglaciation is often associated with significant seasonal insolation differences and/or small latitudinal insolation gradients, and vice versa. We have also noticed a clear correspondence between the rate of G-IG transformation and the difference between seasonal and latitudinal insolation variations. This discovery provides a new perspective for investigating the link between astronomical calculations and paleoclimate data.

In addition, we have examined the influence of insolation on millennial climate variability (MCV) at shorter timescales using high-resolution marine sediment data. While the specific phase and structure of millennial events are mainly dominated by internal forces, their dependence on the background climate state set by insolation is evident as well. Furthermore, the temporospatial variation of insolation distribution seem to have a linear correlation with the timing and frequency of these abrupt events, especially during intermediate glacial periods.

Credit Author Statement

Ziyan Fang: Conceptualization, Methodology, Formal Analysis, Writing, Project Administration, Resources, Visualization.

Feifan Liao: Conceptualization, Methodology, Software, Data Curation, Investigation, Validation, Visualisation.

Zhuoran Fang: Conceptualization, Resources, Data Curation, Formal Analysis.

Zehao Lu: Conceptualization, Software, Resources, Visualisation.

Xuetianhao Wang: Formal Analysis, Software, Resources, Methodology.

Zhuo Ran Fang and Zehao Lu contributed equally as the third author.

References

[1] J. M. Barnola, D. Raynaud, Y. S. Korotkevich, and C. Lorius, ‘Vostok ice core provides 160,000-year record of atmospheric CO2’, Nature, vol. 329, no. 6138, Art. no. 6138, Oct. 1987, doi: 10.1038/329408a0.

[2] J. Imbrie, ‘Astronomical theory of the Pleistocene ice ages: A brief historical review’, Icarus, vol. 50, no. 2, pp. 408–422, May 1982, doi: 10.1016/0019-1035(82)90132-4.

[3] W. F. Ruddiman, Earth’s Climate: past and future. Macmillan, 2001.

[4] M. a. J. Williams, D. L. Dunkerley, P. D. Deckker, A. P. Kershaw, and T. J. Stokes, ‘Quaternary environments’, in Quaternary environments, Edward Arnold Publishers Ltd, 1993. Accessed: Jun. 24, 2023. [Online]. Available: https://research.monash.edu/en/publications/quaternary-environments-2

[5] G. Kukla and J. Gavin, ‘Did glacials start with global warming?’, Quat. Sci. Rev., vol. 24, no. 14, pp. 1547–1557, Aug. 2005, doi: 10.1016/j.quascirev.2004.06.020.

[6] W. S. Broecker and J. van Donk, ‘Insolation changes, ice volumes, and the O 18 record in deep-sea cores’, Rev. Geophys., vol. 8, no. 1, p. 169, 1970, doi: 10.1029/RG008i001p00169.

[7] B. A. S. Davis and S. Brewer, ‘Orbital forcing and role of the latitudinal insolation/temperature gradient’, Clim. Dyn., vol. 32, no. 2, pp. 143–165, Feb. 2009, doi: 10.1007/s00382-008-0480-9.

[8] J. Tian, M. Yang, M. W. Lyle, R. Wilkens, and J. K. Shackford, ‘Obliquity and long eccentricity pacing of the Middle Miocene climate transition’, Geochem. Geophys. Geosystems, vol. 14, no. 6, pp. 1740–1755, 2013, doi: 10.1002/ggge.20108.

[9] G. O’Neill and A. J. Broccoli, ‘Using Linear Reconstructions to Examine the Relative Effects of Variations in Obliquity and Precession on Climate’, vol. 2019, pp. PP22B-10, Dec. 2019.

[10] P. Bajo et al., ‘Persistent influence of obliquity on ice age terminations since the Middle Pleistocene transition’, Science, vol. 367, no. 6483, pp. 1235–1239, Mar. 2020, doi: 10.1126/science.aaw1114.

[11] B. Hobart, L. E. Lisiecki, D. Rand, T. Lee, and C. E. Lawrence, ‘Late Pleistocene 100-kyr glacial cycles paced by precession forcing of summer insolation’, Nat. Geosci., pp. 1–6, Jul. 2023, doi: 10.1038/s41561-023-01235-x.

[12] R. G. Cionco, W. W.-H. Soon, and N. E. Quaranta, ‘On the calculation of latitudinal insolation gradients throughout the Holocene’, Adv. Space Res., vol. 66, no. 3, pp. 720–742, Aug. 2020, doi: 10.1016/j.asr.2020.04.030.

[13] B. J. Harvey, L. C. Shaffrey, and T. J. Woollings, ‘Equator-to-pole temperature differences and the extra-tropical storm track responses of the CMIP5 climate models’, Clim. Dyn., vol. 43, no. 5–6, pp. 1171–1182, Sep. 2014, doi: 10.1007/s00382-013-1883-9.

[14] W. Soon and D. R. Legates, ‘Solar irradiance modulation of Equator-to-Pole (Arctic) temperature gradients: Empirical evidence for climate variation on multi-decadal timescales’, J. Atmospheric Sol.-Terr. Phys., vol. 93, pp. 45–56, Feb. 2013, doi: 10.1016/j.jastp.2012.11.015.

[15] E. W. Wolff, J. Chappellaz, T. Blunier, S. O. Rasmussen, and A. Svensson, ‘Millennial-scale variability during the last glacial: The ice core record’, Quat. Sci. Rev., vol. 29, no. 21–22, pp. 2828–2838, Oct. 2010, doi: 10.1016/j.quascirev.2009.10.013.

[16] D. R. MacAyeal, ‘Binge/purge oscillations of the Laurentide Ice Sheet as a cause of the North Atlantic’s Heinrich events’, Paleoceanography, vol. 8, no. 6, pp. 775–784, 1993, doi: 10.1029/93PA02200.

[17] S. V. Petersen, D. P. Schrag, and P. U. Clark, ‘A new mechanism for Dansgaard-Oeschger cycles’, Paleoceanography, vol. 28, no. 1, pp. 24–30, 2013, doi: 10.1029/2012PA002364.

[18] X. Zhang, G. Lohmann, G. Knorr, and C. Purcell, ‘Abrupt glacial climate shifts controlled by ice sheet changes’, Nature, vol. 512, no. 7514, Art. no. 7514, Aug. 2014, doi: 10.1038/nature13592.

[19] T. M. Dokken, K. H. Nisancioglu, C. Li, D. S. Battisti, and C. Kissel, ‘Dansgaard-Oeschger cycles: Interactions between ocean and sea ice intrinsic to the Nordic seas: D-O CYCLES AS SEEN IN THE NORDIC SEAS’, Paleoceanography, vol. 28, no. 3, pp. 491–502, Sep. 2013, doi: 10.1002/palo.20042.

[20] J. H. Lawton, J. Marotzke, R. Marsh, I. N. McCave, H. Gildor, and E. Tziperman, ‘Sea-ice switches and abrupt climate change’, Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Eng. Sci., vol. 361, no. 1810, pp. 1935–1944, Jul. 2003, doi: 10.1098/rsta.2003.1244.

[21] C. Li, D. S. Battisti, D. P. Schrag, and E. Tziperman, ‘Abrupt climate shifts in Greenland due to displacements of the sea ice edge’, Geophys. Res. Lett., vol. 32, no. 19, 2005, doi: 10.1029/2005GL023492.

[22] C. Li, D. S. Battisti, and C. M. Bitz, ‘Can North Atlantic Sea Ice Anomalies Account for Dansgaard–Oeschger Climate Signals?’, J. Clim., vol. 23, no. 20, pp. 5457–5475, Oct. 2010, doi: 10.1175/2010JCLI3409.1.

[23] R. B. Alley, P. U. Clark, L. D. Keigwin, and R. S. Webb, ‘Making sense of millennial-scale climate change’, Wash. DC Am. Geophys. Union Geophys. Monogr. Ser., vol. 112, pp. 385–394, Jan. 1999, doi: 10.1029/GM112p0385.

[24] M. Yang and J. A. Rial, ‘Internal oscillations of the thermohaline circulation and the Dansgaard-Oeschger events of the last ice age’, vol. 2006, pp. PP23C-1768, Dec. 2006.

[25] W. Broecker, ‘The Great Ocean Conveyor: Discovering the Trigger for Abrupt Climate Change’, in The Great Ocean Conveyor, Princeton University Press, 2010. doi: 10.1515/9781400834716.

[26] L. C. Menviel, L. C. Skinner, L. Tarasov, and P. C. Tzedakis, ‘An ice–climate oscillatory framework for Dansgaard–Oeschger cycles’, Nat. Rev. Earth Environ., vol. 1, no. 12, Art. no. 12, Dec. 2020, doi: 10.1038/s43017-020-00106-y.

[27] E. J. Brook and C. Buizert, ‘Antarctic and global climate history viewed from ice cores’, Nature, vol. 558, no. 7709, pp. 200–208, Jun. 2018, doi: 10.1038/s41586-018-0172-5.

[28] C. Buizert and A. Schmittner, ‘Southern Ocean control of glacial AMOC stability and Dansgaard-Oeschger interstadial duration’, Paleoceanography, vol. 30, no. 12, pp. 1595–1612, 2015, doi: 10.1002/2015PA002795.

[29] Y. Sun et al., ‘Persistent orbital influence on millennial climate variability through the Pleistocene’, Nat. Geosci., vol. 14, no. 11, pp. 812–818, Nov. 2021, doi: 10.1038/s41561-021-00794-1.

[30] X. Zhang et al., ‘Direct astronomical influence on abrupt climate variability’, Nat. Geosci., vol. 14, no. 11, Art. no. 11, Nov. 2021, doi: 10.1038/s41561-021-00846-6.

[31] Kondratyev K. V., ‘Radiation in the Atmosphere’, Int Geophys, 1969.

[32] J. Laskar, A. Fienga, M. Gastineau, and H. Manche, ‘La2010: a new orbital solution for the long-term motion of the Earth’, Astron. Astrophys., vol. 532, p. A89, Aug. 2011, doi: 10.1051/0004-6361/201116836.

[33] Li, M., Hinnov, L.A., and Kump, L.R. 2019. Acycle: Time-series analysis software for paleoclimate projects and education, Computers & Geosciences, 127: 12-22. https://doi.org/10.1016/j.cageo.2019.02.011

[34] C. J. Berends, B. de Boer, and R. S. W. van de Wal, ‘Reconstructing the evolution of ice sheets, sea level, and atmospheric CO2 during the past 3.6 million years’, Clim. Past, vol. 17, no. 1, pp. 361–377, Feb. 2021, doi: 10.5194/cp-17-361-2021.

[35] Kodama, K.P., Hinnov, L.A., 2015. Rock Magnetic Cyclostratigraphy. Wiley-Blackwell,165 p.,https://doi.org/10.1002/9781

[36] D. A. Hodell et al., ‘A 1.5-million-year record of orbital and millennial climate variability in the North Atlantic’, Clim. Past, vol. 19, no. 3, pp. 607–636, Mar. 2023, doi: 10.5194/cp-19-607-2023.

[37] G. J. Kukla, ‘Insolation and glacials’, Boreas, vol. 1, no. 1, pp. 63–96, 1972, doi: 10.1111/j.1502-3885.1972.tb00145.x.

[38] P. Ditlevsen, ‘The Pleistocene Glacial Cycles and Millennial-Scale Climate Variability’, vol. 60, Jun. 2022, Accessed: Aug. 05, 2023. [Online]. Available: https://doi.org/10.1080/07055900.2022.2077172

[39] M. E. Raymo and K. H. Nisancioglu, ‘The 41 kyr world: Milankovitch’s other unsolved mystery’, Paleoceanography, vol. 18, no. 1, 2003, doi: 10.1029/2002PA000791.

[40] G. Vettoretti and W. R. Peltier, ‘Post-Eemian Glacial Inception. Part II: Elements of a Cryospheric Moisture Pump’, J. Clim., vol. 16, no. 6, pp. 912–927, Mar. 2003, doi: 10.1175/1520-0442(2003)016<0912:PEGIPI>2.0.CO;2.

[41] C. S. Jackson and A. J. Broccoli, ‘Orbital forcing of Arctic climate: mechanisms of climate response and implications for continental glaciation’, Clim. Dyn., vol. 21, no. 7, pp. 539–557, Dec. 2003, doi: 10.1007/s00382-003-0351-3.

[42] F. Vimeux, V. Masson, J. Jouzel, M. Stievenard, and J. R. Petit, ‘Glacial–interglacial changes in ocean surface conditions in the Southern Hemisphere’, Nature, vol. 398, no. 6726, Art. no. 6726, Apr. 1999, doi: 10.1038/18860.

[43] V. Masson-Delmotte et al., ‘GRIP Deuterium Excess Reveals Rapid and Orbital-Scale Changes in Greenland Moisture Origin’, Science, vol. 309, no. 5731, pp. 118–121, Jul. 2005, doi: 10.1126/science.1108575.

[44] P. Braconnot et al., ‘Results of PMIP2 coupled simulations of the Mid-Holocene and Last Glacial Maximum – Part 1: experiments and large-scale features’, Clim. Past, vol. 3, no. 2, pp. 261–277, Jun. 2007, doi: 10.5194/cp-3-261-2007.

[45] M.-F. Loutre, D. Paillard, F. Vimeux, and E. Cortijo, ‘Does mean annual insolation have the potential to change the climate?’, Earth Planet. Sci. Lett., vol. 221, no. 1, pp. 1–14, Apr. 2004, doi: 10.1016/S0012-821X(04)00108-6.

[46] N. Rimbu, G. Lohmann, S. J. Lorenz, J. H. Kim, and R. R. Schneider, ‘Holocene climate variability as derived from alkenone sea surface temperature and coupled ocean-atmosphere model experiments’, Clim. Dyn., vol. 23, no. 2, pp. 215–227, Aug. 2004, doi: 10.1007/s00382-004-0435-8.

[47] T. Mitsui and M. Crucifix, ‘Influence of external forcings on abrupt millennial-scale climate changes: a statistical modelling study’, Clim. Dyn., vol. 48, no. 7, pp. 2729–2749, Apr. 2017, doi: 10.1007/s00382-016-3235-z.

[48] J. Rial and M. Yang, ‘Is the Frequency of Abrupt Climate Change Modulated by The Orbital Insolation?’, Geophys Monogr Ser, vol. 173, pp. 167–174, Jan. 2007, doi: 10.1029/173GM12.

[49] B. Martrat et al., ‘Abrupt temperature changes in the Western Mediterranean over the past 250,000 years’, Science, vol. 306, no. 5702, pp. 1762–1765, Dec. 2004, doi: 10.1126/science.1101706.

[50] T. Friedrich, A. Timmermann, L. Menviel, O. Elison Timm, A. Mouchet, and D. M. Roche, ‘The mechanism behind internally generated centennial-to-millennial scale climate variability in an earth system model of intermediate complexity’, Geosci. Model Dev., vol. 3, no. 2, pp. 377–389, 2010, doi: 10.5194/gmd-3-377-2010.

[51] S. M. Olsen, S. Gray, and J. B. Christian, ‘Ocean oxygen isotope constraints on mechanisms for millennial‐scale climate variability’, Paleoceanography, vol. 1, no. 20, Feb. 2005, doi:10.1029/2004PA001063.